Area of Rhombus – Definition & Formula

A rhombus is a two-dimensional or two-dimensional planar figure with an enclosed form or structure. The area of rhombus is thought to be a sort of parallelogram. It is also worth noting that the rhombus has a self-identity as a quadrilateral structure due to its unique features. The other name for a rhombus is an equilateral quadrilateral due to the definition of ‘equilateral,’ which states that all of its sides are always the same length. ‘Rhombus’ is a phrase that was legitimately taken from the ancient Greek word ‘rhombus,’ which denotes something that spins

What is Rhombus?

A rhombus is defined as a quadrilateral with the same length on all four sides in planar Euclidean geometry. Another term for this shape is an equilateral quadrilateral because equilateral indicates that all of its sides are the same length.

A rhombus is properly defined as an exceptional parallelogram due to its parallelogram criteria: it is also defined as a quadrilateral with two sets of parallel sides. Furthermore, a rhombus has 4 equal sides, but it is also a form of a parallelogram with four congruent sides. As a result, a rhombus will fulfill all of the essential criteria of a parallelogram. The qualities of a parallelogram include its four sides staying the same length as well as its opposite sides remaining sufficiently parallel.

So far, we’ve learned about the rhombus. A rhombus, like every other geometric form, possesses qualities that are unique to it. These characteristics distinguish this structure from the other geometrical forms. If you want to study more about different figures, go to straight Cuemath and discover great topics interactively.

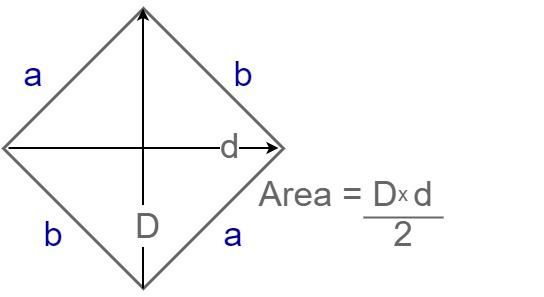
Method 1 for Calculating the Area of a Rhombus Using Diagonals

Consider the rhombus BCDE, which has two diagonals, BC and DE.

• Step 1: Consider the size of diagonal 1, b1. It’s the distance between points B and D. When the diagonals of a rhombus connect at the center, they form four right triangles, which are perpendicular (at 90 degrees to each other) to each other.
• Step 2: Consider the size of diagonal 2, i.e. b2, the distance between the points C and E.
• Step 3: Multiply the b1 and b2 diagonals.
• Step 4: Take the result and divide it by two.

The resulting area of a rhombus ABCD will be given.

Method 2 for Calculating Rhombus Area Using Base & Height

• Step 1: Determine the rhombus’s base and height. The height of the rhombus is the altitude, which is the perpendicular distance from the selected base to the opposing side.
• Step 2: Now in the second step, multiply the computed height by the base.

Are Squares All Rhombus?

Yes, squares are all rhombuses. Since it has 4 equal-length sides, a square is a specific example of a rhombus. All of the angles in a square are right angles which measure 90 degrees, however, not all of the angles in a rhombus must be right angles. As a result, a rhombus with right angles can be thought of as a square.

Examples

Example 1) The base of the rhombus is 5cm & the height of the rhombus is 10cm. Find the area of the rhombus.

Solution) Given, base = 5cm & height = 10cm

Area of the rhombus = height * base

Therefore, the area of the given rhombus = 5 * 10 = 50

Example 2) The two diagonals of a given rhombus have been given to you, diagonal 1 which measures 6 cm, and the other diagonal which measures 10 cm.

Solution) Given, diagonal1 = 6cm & diagonal2 = 10cm

Area of the rhombus = diagonal1* diagonal2

Therefore, the area of the given rhombus = diagonal1 * diagonal2 = 60